東大生と早稲田生のコスパ勉強法【数学・難関大編】

こちらのブログでは、勉強しない勉強法をスローガンに、最小限の努力で合格を目指すコスパ勉強法を紹介しています。

今回のテーマは「数学 難関大ver」です！難関大志望でない方はこちらのコスパ勉強法【数学編】をご覧ください！

理系はもちろん、文系でも避けて通るのは難しい「数学」。

高得点を狙うがゆえに悩みを抱える方は多いと思います。

たった3種類の問題集で数学を極め東大に合格した筆者が、数学のコスパ勉強法を紹介します！

コスパ勉強法に興味を持っていただいた方はぜひコスパ勉強法総編集の記事からご覧ください！

↓　↓　↓　↓　↓

東大生と早稲田生のコスパ勉強法 【総集編】

このサイトでは勉強しない勉強法をテーマにコスパにこだわった勉強法を紹介しています。 教科や目的別の具体的な勉強法は各記事をご覧下さい。 ここでは、コスパ勉強法と…

Not Study | 勉強しない勉強法

簡単な問題と難しい問題の違いとは？？

どうして簡単な問題は解けるのに、難関大の記述問題になると高得点が取れないのでしょうか？

それは、必要な情報が隠されているから！です

数学では解くために使う公式や法則はそこまで多くないです。難問だからといって難しい公式を知らないと解けないということもありません。

ただ、公式の使い方が分かりにくくされているのです。

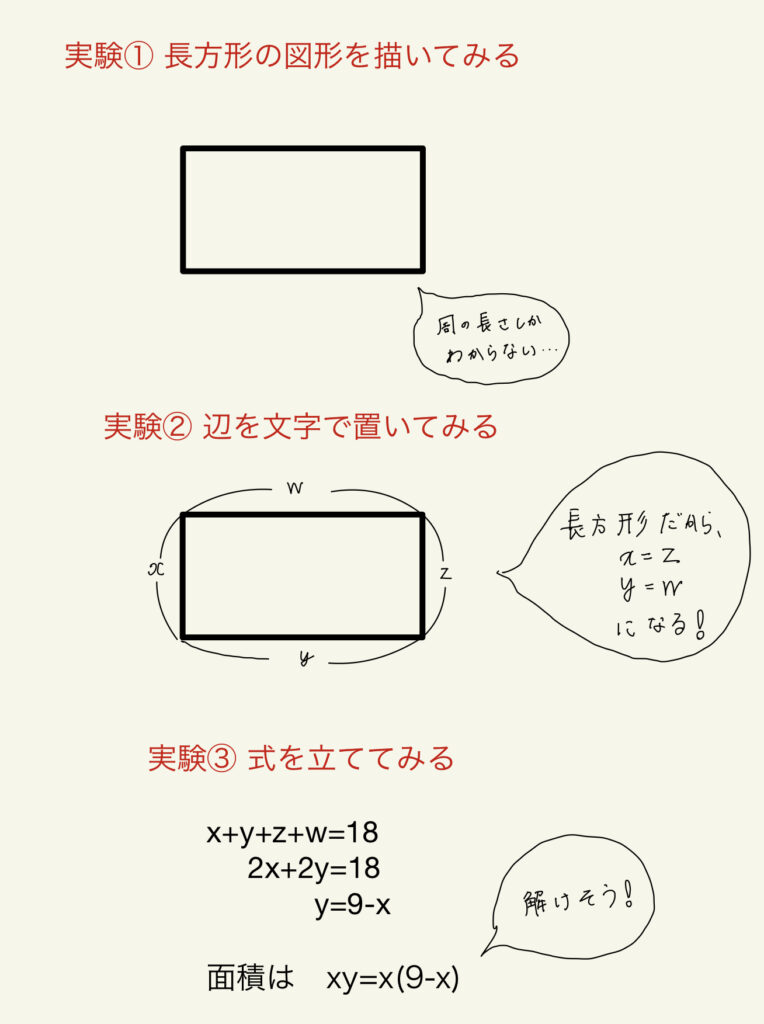
例として、2つの問題を比べてみましょう。

簡単な例ですが、①より②の方が難しいと感じると思います。

でも、本質は同じ。②の問題で一辺をxと置くと①の式が出てきます。

違いは、解くべき式がわかるかわからないかだけです。

解く式は同じなのに、②では式の情報が隠されているのです。

難関大学の数学ではこの情報の隠蔽がハイレベルに行われています。

公式は頭に入っているのに難問が解けないカラクリはお分かりいただけたでしょうか？

では難問を解くにはどうしたらいいのでしょう？

そのカギとなるのが、「実験」です。

難関大数学を解くカギ「実験」とは？

難問を難問たらしめているのは「情報の隠蔽」でした。

ポイントは、式自体が難しいのでは無く式の立て方がわかりにくいだけだったということです。

単純に考えると、わかりにくい問題をわかりやすい問題に捉え直せれば解けるのです！

そのために必要なのが、「実験」です。

「実験」とは、問題をわかりやすくするために、とにかく具体的な数値や文字を代入をしたり、図形を描いてみたりする作業のことです！

先程の問題の問②をもう一度見てみましょう。

簡単な例なので解ける方が多いと思いますが、「実験」を意識して解説してみます。

あとは計算するだけです。解答は最後にまとめてあります。

図を書く、文字で置く、などの基本的な操作をいろいろ試してみたら解けそうな形が見えてくる。

これが「実験」です。

例が簡単すぎましたね。

実験について知ってもらうためにもう一例紹介します。

皆さんならどう解くでしょうか？？

「実験」を理解していればこの問題はとても簡単です。

やってみましょう

こんな簡単に法則を見出せました！

あとは計算するだけ！解答例は最後に載せておきます。

実験の大切さは伝わりましたか？？

以上を踏まえて、難関大数学コスパ勉強法の3ステップを紹介します。

難関大数学コスパ勉強法 3ステップ！

ステップ1 　公式の使い方、使い所の暗記

実験をして法則を見つけても、式が解けなければ意味ないです。典型問題は解けるようにしておきましょう。

今回は上級者向けの記事なのでここの説明は省略します。

ステップ2 　「実験」の練習

この記事のメインはこのステップになります！

このステップの勉強方法としては

①応用問題にたくさん触れる。

②解き始める前にいろいろ試してみる(実験)。

の２つです。ひたすら数をこなして実験に慣れるしかありません。

ただ、やみくもに演習するよりは圧倒的に短期間で実力がつきます！

実験の手法としては上記のようなものがあります！解き始める前にどれかの実験が利用できないか検討してください！

最初は上のリストを意識しながら、徐々に自分なりのアプローチを増やしていきましょう。

「実験」の練習におすすめの参考書がこちら

　↓　↓　↓　↓　↓　↓　↓　↓　↓

別解がたくさん載っているため、模範解にとらわれすぎずとにかく答えにたどり着く姿勢を身に着けられます。ひたすら手を動かして手掛かりを探る「実験」の考え方と近いため、練習にはうってつけの参考書です！

ステップ3 　解ききる練習

「実験」を通して解ける形に持っていけるようになったら、あとは解ききる練習です！

このステップで練習することは、「検算」です。

法則は見つけたのに答えが合わない、、

ということがないように検算の練習をしましょう。

方法は簡単です。ステップ２で使った参考書をもう一度使います。

ステップ２は実験の練習でしたが、今度は検算の練習です。解いたことのある問題なので、絶対に答えを一致させる（ミスをしない）ことだけ意識してください！！

まとめ

いかがだったでしょうか？

今回は難関大学に合格するためのコスパ勉強法を紹介しました。

短期間でハイレベルに！

難関大学を目指すからと言って無駄に時間を費やす必要はありません。むしろ上を目指す人ほど、コスパにこだわって限られた時間を最大限有効活用しましょう。

例題の解答

問題①、②

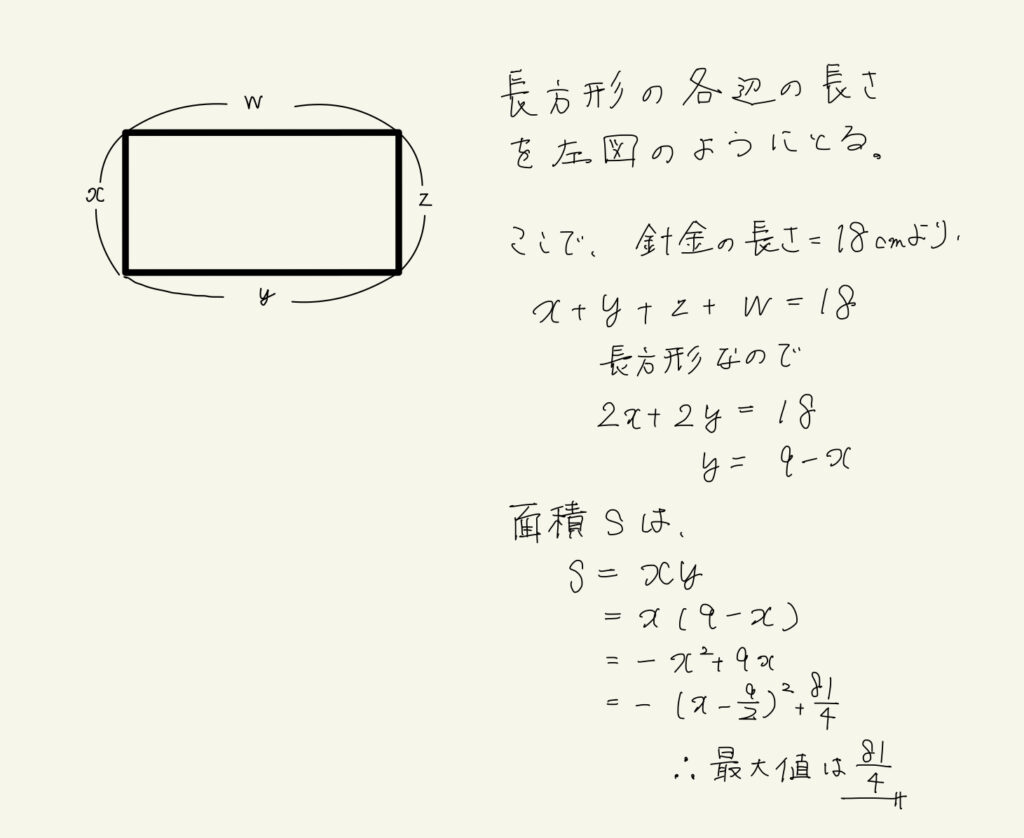
問題

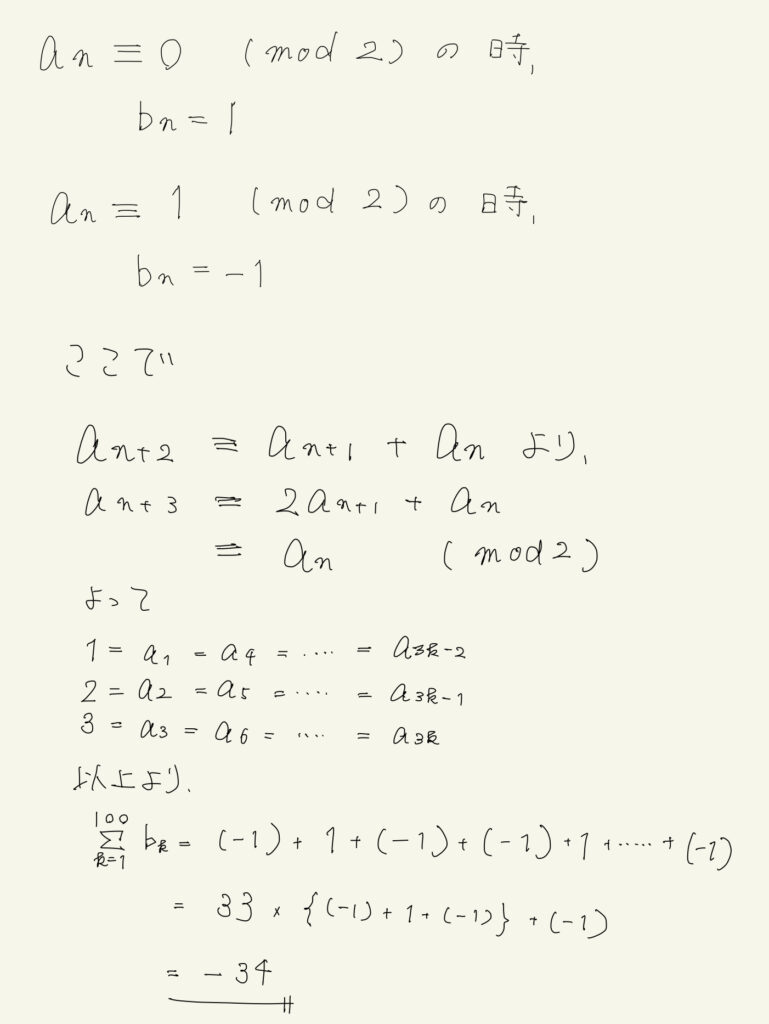
コスパ勉強法や筆者についてもっと知りたい方はぜひ他の記事もご覧ください！